Parábolas

• Una parábola es la representación gráfica de una función cuadrática.
• f(x) = ax² + bx +c

1.  Vértice:

                            

• Por este punto pasa el eje de simetría de la parábola.
• La ecuación del eje de simetría es:
• 

  2. Puntos de corte con el eje OX:

• En el eje de abscisas la segunda coordenada es cero, por lo que tendremos:
• ax² + bx +c = 0

  3. Punto de corte con el eje OY:

• En el eje de ordenadas la primera coordenada es cero, por lo que tendremos:
• f(0) = a· 0² + b· 0 +c = c        

  4. Translaciones de parábolas:

• También podemos representar parábolas a partir de las translaciones de la función: 
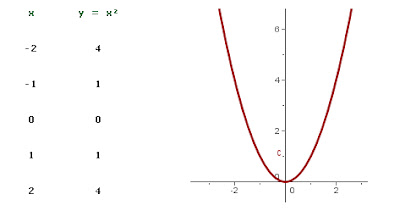
• y = x²
• Ejemplo:

  4.1. Translación vertical:

• y = x² + k
• Si K > 0, y = x² se desplaza hacia arriba k unidades.
• Si K < 0, y = x² se desplaza hacia abajo k unidades.
• El vértice de la parábola es: (0, k).
• El eje de simetría x = 0.
• Ejemplo:
•                 y = x² +2
  
  
  

  4.2. Translación horizontal

• y = (x + h)²
• Si h > 0, y = x² se desplaza hacia la izquierda h unidades.
• Si h < 0, y = x² se desplaza hacia la derecha h unidades.
• El vértice de la parábola es: (-h, 0).
• El eje de simetría es x = -h.
• Ejemplo:             

                            

 

y = (x + 2)²

                  

 

 

5. Ejercicios:

1.

2. 

3.